【理論】平成22年 問13|コイルの内部抵抗を考慮した共振回路の等価並列抵抗の計算問題
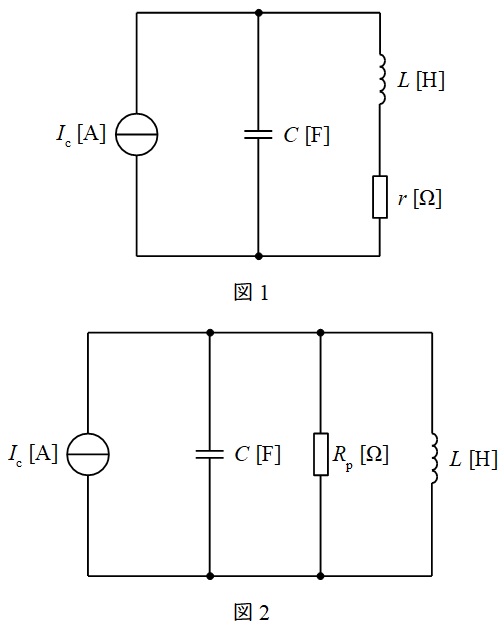
図\( 1 \) は,静電容量 \( C \) \(\mathrm{[F]}\) のコンデンサとコイルからなる共振回路の等価回路である。
このようにコイルに内部抵抗 \( r \) \(\mathrm{[\Omega]}\) が存在する場合は,インダクタンス \( L \) \(\mathrm{[H]}\) と抵抗 \( r \) \(\mathrm{[\Omega]}\) の直列回路として表すことができる。
この直列回路は,コイルの抵抗 \( r \) \(\mathrm{[\Omega]}\) が,誘導性リアクタンス \( \omega L \) \(\mathrm{[\Omega]}\) に比べて十分小さいものとすると,図\( 2 \) のように,等価抵抗 \( R_{\mathrm{p}} \) \(\mathrm{[\Omega]}\) とインダクタンス \( L \) \(\mathrm{[H]}\) の並列回路に変換することができる。
このときの等価抵抗 \( R_{\mathrm{p}} \) \(\mathrm{[\Omega]}\) の値を表す式として,正しいのは次のうちどれか。
ただし,\( I_{\mathrm{c}} \) \(\mathrm{[A]}\) は電流源の電流を表す。
合格への方程式
素子のインピーダンス
インピーダンスは交流回路における「電流の流れにくさ」を表す複素数です。単位はオーム [Ω] です。
基本素子のインピーダンス:
\[ \begin{aligned} \dot{Z}_{\mathrm{R}} &= R \\ \dot{Z}_{\mathrm{L}} &= \mathrm{j}\omega L = \mathrm{j}2\pi f L \\[10pt] \dot{Z}_{\mathrm{C}} &= \frac{1}{\mathrm{j}\omega C} = \frac{1}{\mathrm{j}2\pi f C} \end{aligned} \]
ここで:
- \(R\):抵抗値 [Ω]
- \(L\):インダクタンス [H]
- \(C\):キャパシタンス [F]
- \(\omega\):角周波数 [rad/s]
- \(f\):周波数 [Hz]
- \(\mathrm{j}\):虚数単位(\(\mathrm{j}^2 = -1\))
インピーダンスの特徴:
- 抵抗 (R):周波数に依存せず、常に実数値
- コイル (L):周波数に比例して増加する純虚数(正の虚部)
- コンデンサ (C):周波数に反比例して減少する純虚数(負の虚部)
例題
抵抗 \(R = 100\) [Ω]、インダクタンス \(L = 0.2\) [H]、キャパシタンス \(C = 10\) [μF] について、周波数 \(f = 50\) [Hz] のときのインピーダンスを求めましょう。
まず、角周波数を計算します:
\[ \begin{aligned} \omega = 2\pi f = 2\pi \cdot 50 = 100\pi \text{ [rad/s]} \end{aligned} \]
抵抗のインピーダンス:
\[ \begin{aligned} \dot{Z}_{\mathrm{R}} = R = 100 \text{ [Ω]} \end{aligned} \]
コイルのインピーダンス:
\[ \begin{aligned} \dot{Z}_{\mathrm{L}} &= \mathrm{j}\omega L \\[10pt] &= \mathrm{j} \cdot 100\pi \cdot 0.2 \\[10pt] &= \mathrm{j} \cdot 20\pi \\[10pt] &\approx \mathrm{j} \cdot 62.8 \text{ [Ω]} \end{aligned} \]
コンデンサのインピーダンス(\(C = 10\) [μF] = \(10 \times 10^{-6}\) [F]):
\[ \begin{aligned} \dot{Z}_{\mathrm{C}} &= \frac{1}{\mathrm{j}\omega C} \\[10pt] &= \frac{1}{\mathrm{j} \cdot 100\pi \cdot 10 \times 10^{-6}} \\[10pt] &= \frac{1}{\mathrm{j} \cdot \pi \times 10^{-3}} \\[10pt] &= \frac{-\mathrm{j}}{\pi \times 10^{-3}} \\[10pt] &\approx -\mathrm{j} \cdot 318.3 \text{ [Ω]} \end{aligned} \]
素子のアドミタンス
アドミタンスはインピーダンスの逆数で、交流回路における「電流の流れやすさ」を表す複素数です。単位はジーメンス [S] です。
基本素子のアドミタンス:
\[ \begin{aligned} \dot{Y}_{\mathrm{R}} &= \frac{1}{R} \\[10pt] \dot{Y}_{\mathrm{L}} &= \frac{1}{\mathrm{j}\omega L} = \frac{1}{\mathrm{j}2\pi f L} \\[10pt] \dot{Y}_{\mathrm{C}} &= \mathrm{j}\omega C = \mathrm{j}2\pi f C \end{aligned} \]
アドミタンスの特徴:
- 抵抗 (R):周波数に依存せず、常に実数値
- コイル (L):周波数に反比例して減少する純虚数(負の虚部)
- コンデンサ (C):周波数に比例して増加する純虚数(正の虚部)
アドミタンスの虚部はサセプタンス (B) と呼ばれ、実部はコンダクタンス (G) と呼ばれます。
\[ \begin{aligned} \dot{Y} = G + \mathrm{j}B \end{aligned} \]
例題
先ほどと同じ素子について、アドミタンスを求めましょう。
抵抗のアドミタンス:
\[ \begin{aligned} \dot{Y}_{\mathrm{R}} &= \frac{1}{R} \\[10pt] &= \frac{1}{100} \\[10pt] &= 0.01 \text{ [S]} \end{aligned} \]
コイルのアドミタンス:
\[ \begin{aligned} \dot{Y}_{\mathrm{L}} &= \frac{1}{\dot{Z}_{\mathrm{L}}} \\[10pt] &= \frac{1}{\mathrm{j} \cdot 62.8} \\[10pt] &= \frac{-\mathrm{j}}{62.8} \\[10pt] &\approx -\mathrm{j} \cdot 0.0159 \text{ [S]} \end{aligned} \]
コンデンサのアドミタンス:
\[ \begin{aligned} \dot{Y}_{\mathrm{C}} &= \frac{1}{\dot{Z}_{\mathrm{C}}} \\[10pt] &= \frac{1}{-\mathrm{j} \cdot 318.3} \\[10pt] &= \frac{\mathrm{j}}{318.3} \\[10pt] &\approx \mathrm{j} \cdot 0.0031 \text{ [S]} \end{aligned} \]
または、直接公式から:
\[ \begin{aligned} \dot{Y}_{\mathrm{C}} &= \mathrm{j}\omega C \\[10pt] &= \mathrm{j} \cdot 100\pi \cdot 10 \times 10^{-6} \\[10pt] &= \mathrm{j} \cdot \pi \times 10^{-3} \\[10pt] &\approx \mathrm{j} \cdot 0.0031 \text{ [S]} \end{aligned} \]
合成インピーダンス
合成インピーダンスの計算式:
① 直列接続:
\[ \begin{aligned} \dot{Z} &= \dot{Z}_1 + \dot{Z}_2 \end{aligned} \]
② 並列接続:
\[ \begin{aligned} \frac{1}{\dot{Z}} &= \frac{1}{\dot{Z}_1} + \frac{1}{\dot{Z}_2} \\[10pt] \dot{Z} &= \frac{\dot{Z}_1 \dot{Z}_2}{\dot{Z}_1 + \dot{Z}_2} \end{aligned} \]
合成インピーダンスの特徴:
- 直列接続:素子に同じ電流が流れ、各素子の電圧の和が全体の電圧となる
- 並列接続:素子に同じ電圧がかかり、各素子の電流の和が全体の電流となる
例題
抵抗 \(R = 50\) [Ω] とコイル \(L = 0.1\) [H] が直列に接続されている場合の、周波数 \(f = 60\) [Hz] における合成インピーダンスを求めましょう。
コイルのインピーダンス:
\[ \begin{aligned} \dot{Z}_{\mathrm{L}} &= \mathrm{j}\omega L \\[10pt] &= \mathrm{j} \cdot 2\pi \cdot 60 \cdot 0.1 \\[10pt] &= \mathrm{j} \cdot 37.7 \text{ [Ω]} \end{aligned} \]
直列接続の合成インピーダンス:
\[ \begin{aligned} \dot{Z} &= R + \dot{Z}_{\mathrm{L}} \\[10pt] &= 50 + \mathrm{j} \cdot 37.7 \text{ [Ω]} \end{aligned} \]
合成インピーダンスの大きさと位相:
\[ \begin{aligned} |\dot{Z}| &= \sqrt{50^2 + 37.7^2} \approx 62.7 \text{ [Ω]} \\[10pt] \theta &= \tan^{-1}\left(\frac{37.7}{50}\right) \approx 37.0° \text{ または } 0.646 \text{ [rad]} \end{aligned} \]
例題2:並列接続
抵抗 \(R = 200\) [Ω] とコンデンサ \(C = 5\) [μF] が並列に接続されている場合の、周波数 \(f = 50\) [Hz] における合成インピーダンスを求めましょう。
コンデンサのインピーダンス:
\[ \begin{aligned} \dot{Z}_{\mathrm{C}} &= \frac{1}{\mathrm{j}\omega C} \\[10pt] &= \frac{1}{\mathrm{j} \cdot 2\pi \cdot 50 \cdot 5 \times 10^{-6}} \\[10pt] &\approx -\mathrm{j} \cdot 636.6 \text{ [Ω]} \end{aligned} \]
並列接続の合成インピーダンス:
\[ \begin{aligned} \dot{Z} &= \frac{\dot{Z}_{\mathrm{R}} \dot{Z}_{\mathrm{C}}}{\dot{Z}_{\mathrm{R}} + \dot{Z}_{\mathrm{C}}} \\[10pt] &= \frac{200 \cdot (-\mathrm{j} \cdot 636.6)}{200 + (-\mathrm{j} \cdot 636.6)} \\[10pt] &= \frac{-\mathrm{j} \cdot 127320}{200 - \mathrm{j} \cdot 636.6} \end{aligned} \]
分母と分子に分母の共役複素数を掛けて整理します:
\[ \begin{aligned} \dot{Z} &= \frac{-\mathrm{j} \cdot 127320 \cdot (200 + \mathrm{j} \cdot 636.6)}{(200 - \mathrm{j} \cdot 636.6) \cdot (200 + \mathrm{j} \cdot 636.6)} \\[10pt] &= \frac{-\mathrm{j} \cdot 127320 \cdot (200 + \mathrm{j} \cdot 636.6)}{200^2 + 636.6^2} \\[10pt] &= \frac{-\mathrm{j} \cdot 25464000 - \mathrm{j}^2 \cdot 81043512}{40000 + 405304} \\[10pt] &= \frac{-\mathrm{j} \cdot 25464000 + 81043512}{445304} \\[10pt] &\approx 182.0 - \mathrm{j} \cdot 57.2 \text{ [Ω]} \end{aligned} \]
合成アドミタンス
合成アドミタンスの計算式:
① 直列接続:
\[ \begin{aligned} \frac{1}{\dot{Y}} &= \frac{1}{\dot{Y}_1} + \frac{1}{\dot{Y}_2} \\[10pt] \dot{Y} &= \frac{\dot{Y}_1 \dot{Y}_2}{\dot{Y}_1 + \dot{Y}_2} \end{aligned} \]
② 並列接続:
\[ \begin{aligned} \dot{Y} &= \dot{Y}_1 + \dot{Y}_2 \end{aligned} \]
合成アドミタンスの特徴:
- 直列接続のインピーダンス計算式と並列接続のアドミタンス計算式が同じ形
- 並列接続のインピーダンス計算式と直列接続のアドミタンス計算式が同じ形
- アドミタンスで計算すると並列接続の合成が特に簡単になる
例題
抵抗 \(R = 50\) [Ω] とコンデンサ \(C = 20\) [μF] が並列に接続されている場合の、周波数 \(f = 50\) [Hz] における合成アドミタンスを求めましょう。
抵抗のアドミタンス:
\[ \begin{aligned} \dot{Y}_{\mathrm{R}} &= \frac{1}{R} \\[10pt] &= \frac{1}{50} \\[10pt] &= 0.02 \text{ [S]} \end{aligned} \]
コンデンサのアドミタンス:
\[ \begin{aligned} \dot{Y}_{\mathrm{C}} &= \mathrm{j}\omega C \\[10pt] &= \mathrm{j} \cdot 2\pi \cdot 50 \cdot 20 \times 10^{-6} \\[10pt] &= \mathrm{j} \cdot 0.00628 \text{ [S]} \end{aligned} \]
並列接続の合成アドミタンス:
\[ \begin{aligned} \dot{Y} &= \dot{Y}_{\mathrm{R}} + \dot{Y}_{\mathrm{C}} \\[10pt] &= 0.02 + \mathrm{j} \cdot 0.00628 \text{ [S]} \end{aligned} \]
合成アドミタンスの大きさと位相:
\[ \begin{aligned} |\dot{Y}| &= \sqrt{0.02^2 + 0.00628^2} \approx 0.0209 \text{ [S]} \\[10pt] \theta &= \tan^{-1}\left(\frac{0.00628}{0.02}\right) \approx 17.4° \text{ または } 0.304 \text{ [rad]} \end{aligned} \]
合成インピーダンスに変換すると:
\[ \begin{aligned} \dot{Z} &= \frac{1}{\dot{Y}} \\[10pt] &= \frac{1}{0.02 + \mathrm{j} \cdot 0.00628} \\[10pt] &\approx 47.8 - \mathrm{j} \cdot 15.0 \text{ [Ω]} \end{aligned} \]
🔍 ワンポイントアドバイス: インピーダンスとアドミタンスは互いに逆数の関係にあります。直列回路はインピーダンスで計算すると簡単になり、並列回路はアドミタンスで計算すると簡単になります。複雑な回路では、適切な方法を選ぶことで計算を効率化できます。また、複素数の計算に慣れることも重要です。計算の際には \(\mathrm{j}^2 = -1\) であることを忘れないようにしましょう。
今回はコイルとコンデンサと抵抗が混在する回路の問題やな。まずはインピーダンスとアドミタンスについて基本から確認しとこか。インピーダンスとアドミタンスの関係、わかるか?
はい、先生!インピーダンスとアドミタンスは互いに逆数の関係にあります。
インピーダンス Z は交流回路における「抵抗」の概念を拡張したもので、単位はΩ(オーム)です。
アドミタンス Y はインピーダンスの逆数で、「導電率」に相当します。単位はS(ジーメンス)です。
\( Y = \frac{1}{Z} \)ええやん!じゃあ次に、問題にある図1の回路を考えるで。これはどんな回路になってるんやろ?
図1の回路は、コンデンサC(容量リアクタンス)と、直列に接続された抵抗rとコイルL(誘導リアクタンス)の並列回路です。
つまり、コンデンサCが、抵抗rとコイルLの直列回路と並列に接続された構造になっています。
そうやな!まずは抵抗rとコイルLの直列回路の合成インピーダンスZ₁を考えるで。これはどうなる?
抵抗rとコイルLの直列回路の合成インピーダンスZ₁は、それぞれのインピーダンスの和になります。
抵抗rのインピーダンスは単純にr [Ω]
コイルLのインピーダンスはjωL [Ω] (jは虚数単位)
\[ \begin{aligned} \dot{Z}_1 &= r + j\omega L \end{aligned} \]この式は、実部r(抵抗成分)と虚部jωL(リアクタンス成分)を持つ複素数として表されます。
ナイスや!次に図1の回路全体の合成アドミタンスY₁を求めるんやけど、どないして求めたらええと思う?
図1の回路全体の合成アドミタンスY₁を求めるには、並列接続されている各素子のアドミタンスを足し合わせます。
コンデンサCのアドミタンスは jωC [S]
抵抗rとコイルLの直列回路のアドミタンスは 1/Z₁ = 1/(r + jωL) [S]
\[ \begin{aligned} \dot{Y}_1 &= j\omega C + \frac{1}{\dot{Z}_1} \\[10pt] &= j\omega C + \frac{1}{r + j\omega L} \end{aligned} \]そのとおり!でも1/(r + jωL)はこのままやと扱いにくいな。分母に虚数jがあるから、有理化せなあかんで。どないやったかな?
はい、分母を有理化するには分子・分母に分母の共役複素数をかけます。
\[ \begin{aligned} \frac{1}{r + j\omega L} &= \frac{1}{r + j\omega L} \times \frac{r - j\omega L}{r - j\omega L} \\[10pt] &= \frac{r - j\omega L}{(r + j\omega L)(r - j\omega L)} \\[10pt] &= \frac{r - j\omega L}{r^2 + (\omega L)^2} \end{aligned} \]これで分母が実数になりました。
よっしゃ!じゃあこれを使って合成アドミタンスY₁の式を続けてみよか。
合成アドミタンスY₁の計算を続けます。
\[ \begin{aligned} \dot{Y}_1 &= j\omega C + \frac{1}{r + j\omega L} \\[10pt] &= j\omega C + \frac{r - j\omega L}{r^2 + (\omega L)^2} \\[10pt] &= j\omega C + \frac{r}{r^2 + (\omega L)^2} - j\frac{\omega L}{r^2 + (\omega L)^2} \\[10pt] &= \frac{r}{r^2 + (\omega L)^2} + j\left(\omega C - \frac{\omega L}{r^2 + (\omega L)^2}\right) \end{aligned} \]これで合成アドミタンスY₁が求まりました。実部は導電成分(G)、虚部はサセプタンス成分(B)を表しています。
ナイス計算や!問題では「ωL ≫ r」つまりコイルのリアクタンスが抵抗よりもずっと大きい条件やから、式を近似してみるで。この場合、どう近似できるかな?
「ωL ≫ r」の条件では、分母の r² + (ωL)² において r²は(ωL)²に比べて非常に小さいので無視できます。
\[ \begin{aligned} r^2 + (\omega L)^2 &\approx (\omega L)^2 \\ \end{aligned} \]この近似を使って、Y₁の式を簡略化します:
\[ \begin{aligned} \dot{Y}_1 &\approx \frac{r}{(\omega L)^2} + j\left(\omega C - \frac{\omega L}{(\omega L)^2}\right) \\[10pt] &= \frac{r}{(\omega L)^2} + j\left(\omega C - \frac{1}{\omega L}\right) \end{aligned} \]ようやっとるな!次に図2の回路を考えるで。これはどんな回路になってるか説明してみてくれるか?
図2の回路は、抵抗Rp、コンデンサC、コイルLが全て並列に接続された回路です。これは並列回路なので、アドミタンスを使って計算するのが便利です。
せやな!じゃあ図2の回路の合成アドミタンスY₂を求めてみよか。
図2の回路では、素子がすべて並列接続されているので、合成アドミタンスY₂は各素子のアドミタンスの和になります。
抵抗Rpのアドミタンス: 1/Rp [S]
コンデンサCのアドミタンス: jωC [S]
コイルLのアドミタンス: 1/(jωL) = -j/(ωL) [S]
\[ \begin{aligned} \dot{Y}_2 &= \frac{1}{R_p} + j\omega C + \frac{1}{j\omega L} \\[10pt] &= \frac{1}{R_p} + j\omega C + \frac{1}{j\omega L} \times \frac{j}{j} \\[10pt] &= \frac{1}{R_p} + j\omega C - \frac{j}{\omega L} \\[10pt] &= \frac{1}{R_p} + j\left(\omega C - \frac{1}{\omega L}\right) \end{aligned} \]完璧やな!さて、この問題のポイントは、図1と図2の回路が等価であるという条件や。Y₁とY₂が等しいってことは、どういうことになる?
図1と図2の回路が等価であるためには、両回路の合成アドミタンス(Y₁とY₂)が等しくなければなりません。
Y₁とY₂の式を比較すると:
\[ \begin{aligned} \dot{Y}_1 &= \frac{r}{(\omega L)^2} + j\left(\omega C - \frac{1}{\omega L}\right) \\[10pt] \dot{Y}_2 &= \frac{1}{R_p} + j\left(\omega C - \frac{1}{\omega L}\right) \end{aligned} \]これらが等しいためには、実部同士、虚部同士が等しくなければなりません。
虚部は既に同じ形になっていますので、実部を比較します:
\[ \begin{aligned} \frac{r}{(\omega L)^2} &= \frac{1}{R_p} \\ \end{aligned} \]そうや!じゃあこの式からRpを求めてみよか。
Rpを求めるために、方程式を変形します。
\[ \begin{aligned} \frac{r}{(\omega L)^2} &= \frac{1}{R_p} \\[10pt] r \cdot R_p &= (\omega L)^2 \\[10pt] R_p &= \frac{(\omega L)^2}{r} \end{aligned} \]したがって、Rp = (ωL)²/r となります。これが選択肢(4)に対応します。
よっしゃ!これで完璧や。最後にこの問題を通して学んだ重要なポイントをまとめてみよか?
はい、先生!この問題から学んだ重要なポイントは:
1. 直列回路と並列回路の等価変換:実際の回路を別の形の等価回路に置き換えることで、解析が容易になることがあります。
2. インピーダンスとアドミタンス:直列回路ではインピーダンス、並列回路ではアドミタンスを使うと計算が簡単になります。
3. 複素数の取り扱い:交流回路の計算では、複素数の四則演算や有理化などの操作が必要です。
4. 比較による方程式の導出:等価回路の条件から、実部同士、虚部同士を比較して方程式を立てることができます。
5. 近似計算:「ωL ≫ r」のような条件がある場合、適切な近似を行うことで計算を簡略化できます。
この問題では、RL直列回路とコンデンサの並列接続を、RLC並列回路に変換する際の抵抗値の関係式Rp = (ωL)²/rを導出しました。
解説まとめ
抵抗 \( r \)[Ω] とインダクタンス \( \omega L \) [Ω] の直列接続の合成インピーダンス \( \dot{Z}_1 \)[Ω] は、次のように表される。
\[ \dot{Z}_1 = r + \mathrm{j} \omega L \]
したがって、図1の合成アドミタンス \( \dot{Y}_1 \)[S] は以下のようになる:
\[ \begin{aligned} \dot{Y}_1 &= \mathrm{j} \omega C + \frac{1}{\dot{Z}_1} \\ &= \mathrm{j} \omega C + \frac{1}{r + \mathrm{j} \omega L} \\ &= \mathrm{j} \omega C + \frac{1}{r + \mathrm{j} \omega L} \times \frac{r - \mathrm{j} \omega L}{r - \mathrm{j} \omega L} \\ &= \mathrm{j} \omega C + \frac{r - \mathrm{j} \omega L}{r^2 + (\omega L)^2} \\ &= \frac{r}{r^2 + (\omega L)^2} + \mathrm{j} \left( \omega C - \frac{\omega L}{r^2 + (\omega L)^2} \right) \end{aligned} \]
ここで、\( \omega L \gg r \)であると仮定すると、近似的に:
\[ \begin{aligned} \dot{Y}_1 &\simeq \frac{r}{(\omega L)^2} + \mathrm{j} \left( \omega C - \frac{1}{\omega L} \right) \end{aligned} \]
また、図2の合成アドミタンス \( \dot{Y}_2 \) [S] は次のように求められる:
\[ \begin{aligned} \dot{Y}_2 &= \mathrm{j} \omega C + \frac{1}{R_{\mathrm{p}}} + \frac{1}{\mathrm{j} \omega L} \\ &= \frac{1}{R_{\mathrm{p}}} + \mathrm{j} \left( \omega C - \frac{1}{\omega L} \right) \\ &\quad \left( \because \frac{1}{\mathrm{j}} = -\mathrm{j} \right) \end{aligned} \]
\( \dot{Y}_1 \) と \( \dot{Y}_2 \)は等しくなければならないため、係数を比較すると:
\[ \begin{aligned} \frac{r}{(\omega L)^2} &= \frac{1}{R_{\mathrm{p}}} \\ R_{\mathrm{p}} &= \frac{(\omega L)^2}{r} \end{aligned} \]